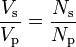Transformer

From Wikipedia, the free encyclopedia

This article is about the electrical device . For the toy line franchise, see Transformers. For other uses, see Transformer (disambiguation).

Pole-mounted power distribution transformer with center-tapped secondary winding (note use of grounded conductor, right, as one leg of the primary feeder). It transforms the high voltage of the overhead distribution wires to the lower voltage used in house wiring.

A transformer is a static device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field through the secondary winding. This varying magnetic field induces a varying electromotive force (EMF) or "voltage" in the secondary winding. This effect is called mutual induction.

If a load is connected to the secondary, an electric current will flow in the secondary winding and electrical energy will be transferred from the primary circuit through the transformer to the load. In an ideal transformer, the induced voltage in the secondary winding (V_s) is in proportion to the primary voltage (V_p), and is given by the ratio of the number of turns in the secondary (N_s) to the number of turns in the primary (N_p) as follows:

$\frac{V_\text{s}}{V_{\text{p}}} = \frac{N_\text{s}}{N_\text{p}}$

By appropriate selection of the ratio of turns, a transformer thus allows an alternating current (AC) voltage to be "stepped up" by making N_s greater than N_p, or "stepped down" by making N_s less than N_p.

In the vast majority of transformers, the windings are coils wound around a ferromagnetic core, air-core transformers being a notable exception.

Transformers range in size from a thumbnail-sized coupling transformer hidden inside a stage microphone to huge units weighing hundreds of tons used to interconnect portions of power grids. All operate with the same basic principles, although the range of designs is wide. While new technologies have eliminated the need for transformers in some electronic circuits, transformers are still found in nearly all electronic devices designed for household ("mains") voltage. Transformers are essential for high-voltage electric power transmission, which makes long-distance transmission economically practical.

[hide]

[edit] History

[edit] Discovery

Faraday's experiment with induction between coils of wire ^[1]

The phenomenon of electromagnetic induction was discovered independently by Michael Faraday and Joseph Henry in 1831. However, Faraday was the first to publish the results of his experiments and thus receive credit for the discovery.^[2] The relationship between electromotive force (EMF) or "voltage" and magnetic flux was formalized in an equation now referred to as "Faraday's law of induction":

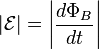$|\mathcal{E}| = \left|{{d\Phi_B} \over dt}\right|$ .

where 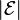$|\mathcal{E}|$ is the magnitude of the EMF in volts and Φ_B is the magnetic flux through the circuit (in webers).^[3]

Faraday performed the first experiments on induction between coils of wire, including winding a pair of coils around an iron ring, thus creating the first toroidal closed-core transformer.^[4]

[edit] Induction coils

Faraday's ring transformer

The first type of transformer to see wide use was the induction coil, invented by Rev. Nicholas Callan of Maynooth College, Ireland in 1836. He was one of the first researchers to realize that the more turns the secondary winding has in relation to the primary winding, the larger is the increase in EMF. Induction coils evolved from scientists' and inventors' efforts to get higher voltages from batteries. Since batteries produce direct current (DC) rather than alternating current (AC), induction coils relied upon vibrating electrical contacts that regularly interrupted the current in the primary to create the flux changes necessary for induction. Between the 1830s and the 1870s, efforts to build better induction coils, mostly by trial and error, slowly revealed the basic principles of transformers.

By the 1870s, efficient generators that produced alternating current (alternators) were available, and it was found that alternating current could power an induction coil directly, without an interrupter. In 1876, Russian engineer Pavel Yablochkov invented a lighting system based on a set of induction coils where the primary windings were connected to a source of alternating current and the secondary windings could be connected to several "electric candles" (arc lamps) of his own design.^[5]^[6] The coils Yablochkov employed functioned essentially as transformers.^[5]

In 1878, the Ganz Company in Hungary began manufacturing equipment for electric lighting and, by 1883, had installed over fifty systems in Austria-Hungary. Their systems used alternating current exclusively and included those comprising both arc and incandescent lamps, along with generators and other equipment.^[7]

Lucien Gaulard and John Dixon Gibbs first exhibited a device with an open iron core called a "secondary generator" in London in 1882, then sold the idea to the Westinghouse company in the United States.^[8] They also exhibited the invention in Turin, Italy in 1884, where it was adopted for an electric lighting system.^[9] However, the efficiency of their open-core bipolar apparatus remained very low.^[10]

Induction coils with open magnetic circuits are inefficient for transfer of power to loads. Until about 1880, the paradigm for AC power transmission from a high voltage supply to a low voltage load was a series circuit. Open-core transformers with a ratio near 1:1 were connected with their primaries in series to allow use of a high voltage for transmission while presenting a low voltage to the lamps. The inherent flaw in this method was that turning off a single lamp affected the voltage supplied to all others on the same circuit. Many adjustable transformer designs were introduced to compensate for this problematic characteristic of the series circuit, including those employing methods of adjusting the core or bypassing the magnetic flux around part of a coil.^[11]

Efficient, practical transformer designs did not appear until the 1880s, but within a decade the transformer would be instrumental in the "War of Currents", and in seeing AC distribution systems triumph over their DC counterparts, a position in which they have remained dominant ever since.^[12]

[edit] Closed-core transformers and the introduction of parallel connection

Drawing of Ganz Company's 1885 prototype. Capacity: 1400 VA, frequency: 40 Hz, voltage ratio: 120/72 V

Prototypes of the world's first high-efficiency transformers. They were built by the Z.B.D. team on 16th September 1884.^[13]

In the autumn of 1884,^[14] Ganz Company engineers Károly Zipernowsky, Ottó Bláthy and Miksa Déri had determined that open-core devices were impracticable, as they were incapable of reliably regulating voltage. In their joint patent application for the "Z.B.D." transformers, they described two designs with closed magnetic circuits: the "closed-core" and "shell-core" transformers. In the closed-core, the primary and secondary windings were wound around a closed iron ring; in the shell-core, the windings were passed through the iron core. In both designs, the magnetic flux linking the primary and secondary windings traveled almost entirely within the iron core, with no intentional path through air. The new Z.B.D. transformers reached 98 percent efficiency, which was 3.4 times higher than the open core bipolar devices of Gaulard and Gibs.^[15] When they employed it in parallel connected electric distribution systems, closed-core transformers finally made it technically and economically feasible to provide electric power for lighting in homes, businesses and public spaces.^[16]^[17] Bláthy had suggested the use of closed-cores, Zipernowsky the use of shunt connections, and Déri had performed the experiments;^[18] Bláthy also discovered the transformer formula, Vs/Vp = Ns/Np.^{[citation needed]} The vast majority of transformers in use today rely on the basic principles discovered by the three engineers. They also reportedly popularized the word "transformer" to describe a device for altering the EMF of an electric current,^[16]^[19] although the term had already been in use by 1882.^[20]^[21] In 1886, the Ganz Company installed the world's first power station that used AC generators to power a parallel-connected common electrical network, the steam-powered Rome-Cerchi power plant.^[22]

Stanley's 1886 design for adjustable gap open-core induction coils^[23]

Although George Westinghouse had bought Gaulard and Gibbs' patents in 1885, the Edison Electric Light Company held an option on the U.S. rights for the Z.B.D. transformers, requiring Westinghouse to pursue alternative designs on the same principles. He assigned to William Stanley the task of developing a device for commercial use in United States.^[24] Stanley's first patented design was for induction coils with single cores of soft iron and adjustable gaps to regulate the EMF present in the secondary winding. (See drawing at left.)^[23] This design was first used commercially in the U.S. in 1886.^[12] But Westinghouse soon had his team working on a design whose core comprised a stack of thin "E-shaped" iron plates, separated individually or in pairs by thin sheets of paper or other insulating material. Prewound copper coils could then be slid into place, and straight iron plates laid in to create a closed magnetic circuit. Westinghouse applied for a patent for the new design in December 1886; it was granted in July 1887.^[18]^[25]

[edit] Other early transformers

In 1889, Russian-born engineer Mikhail Dolivo-Dobrovolsky developed the first three-phase transformer at the Allgemeine Elektricitäts-Gesellschaft ("General Electricity Company") in Germany.^[26]

In 1891, Nikola Tesla invented the Tesla coil, an air-cored, dual-tuned resonant transformer for generating very high voltages at high frequency.^[27]^[28]

Audio frequency transformers ("repeating coils") were used by early experimenters in the development of the telephone.^{[citation needed]}

[edit] Basic principles

The transformer is based on two principles: first, that an electric current can produce a magnetic field (electromagnetism), and, second that a changing magnetic field within a coil of wire induces a voltage across the ends of the coil (electromagnetic induction). Changing the current in the primary coil changes the magnetic flux that is developed. The changing magnetic flux induces a voltage in the secondary coil.

An ideal transformer

An ideal transformer is shown in the adjacent figure. Current passing through the primary coil creates a magnetic field. The primary and secondary coils are wrapped around a core of very high magnetic permeability, such as iron, so that most of the magnetic flux passes through both the primary and secondary coils.

[edit] Induction law

The voltage induced across the secondary coil may be calculated from Faraday's law of induction, which states that:

$V_\text{s} = N_\text{s} \frac{\mathrm{d}\Phi}{\mathrm{d}t},$

where V_s is the instantaneous voltage, N_s is the number of turns in the secondary coil and Φ is the magnetic flux through one turn of the coil. If the turns of the coil are oriented perpendicular to the magnetic field lines, the flux is the product of the magnetic flux density B and the area A through which it cuts. The area is constant, being equal to the cross-sectional area of the transformer core, whereas the magnetic field varies with time according to the excitation of the primary. Since the same magnetic flux passes through both the primary and secondary coils in an ideal transformer,^[29] the instantaneous voltage across the primary winding equals

$V_\text{p} = N_\text{p} \frac{\mathrm{d}\Phi}{\mathrm{d}t}.$

Taking the ratio of the two equations for V_s and V_p gives the basic equation^[30] for stepping up or stepping down the voltage

$\frac{V_\text{s}}{V_\text{p}} = \frac{N_\text{s}}{N_\text{p}}.$

N_p/N_s is known as the turns ratio, and is the primary functional characteristic of any transformer. In the case of step-up transformers, this may sometimes be stated as the reciprocal, N_s/N_p. Turns ratio is commonly expressed as an irreducible fraction or ratio: for example, a transformer with primary and secondary windings of, respectively, 100 and 150 turns is said to have a turns ratio of 2:3 rather than 0.667 or 100:150.

[edit] Ideal power equation

The ideal transformer as a circuit element

If the secondary coil is attached to a load that allows current to flow, electrical power is transmitted from the primary circuit to the secondary circuit. Ideally, the transformer is perfectly efficient; all the incoming energy is transformed from the primary circuit to the magnetic field and into the secondary circuit. If this condition is met, the incoming electric power must equal the outgoing power:

$P_\text{incoming} = I_\text{p} V_\text{p} = P_\text{outgoing} = I_\text{s} V_\text{s},\!$

giving the ideal transformer equation

$\frac{V_\text{s}}{V_\text{p}} = \frac{N_\text{s}}{N_\text{p}} = \frac{I_\text{p}}{I_\text{s}}.$

Transformers normally have high efficiency, so this formula is a reasonable approximation.

If the voltage is increased, then the current is decreased by the same factor. The impedance in one circuit is transformed by the square of the turns ratio.^[29] For example, if an impedance Z_s is attached across the terminals of the secondary coil, it appears to the primary circuit to have an impedance of (N_p/N_s)²Z_s. This relationship is reciprocal, so that the impedance Z_p of the primary circuit appears to the secondary to be (N_s/N_p)²Z_p.

[edit] Detailed operation

The simplified description above neglects several practical factors, in particular the primary current required to establish a magnetic field in the core, and the contribution to the field due to current in the secondary circuit.

Models of an ideal transformer typically assume a core of negligible reluctance with two windings of zero resistance.^[31] When a voltage is applied to the primary winding, a small current flows, driving flux around the magnetic circuit of the core.^[31] The current required to create the flux is termed the magnetizing current; since the ideal core has been assumed to have near-zero reluctance, the magnetizing current is negligible, although still required to create the magnetic field.

The changing magnetic field induces an electromotive force (EMF) across each winding.^[32] Since the ideal windings have no impedance, they have no associated voltage drop, and so the voltages V_P and V_S measured at the terminals of the transformer, are equal to the corresponding EMFs. The primary EMF, acting as it does in opposition to the primary voltage, is sometimes termed the "back EMF".^[33] This is due to Lenz's law which states that the induction of EMF would always be such that it will oppose development of any such change in magnetic field.

[edit] Practical considerations

[edit] Leakage flux

Leakage flux of a transformer

Main article: Leakage inductance

The ideal transformer model assumes that all flux generated by the primary winding links all the turns of every winding, including itself. In practice, some flux traverses paths that take it outside the windings.^[34] Such flux is termed leakage flux, and results in leakage inductance in series with the mutually coupled transformer windings.^[33] Leakage results in energy being alternately stored in and discharged from the magnetic fields with each cycle of the power supply. It is not directly a power loss (see "Stray losses" below), but results in inferior voltage regulation, causing the secondary voltage to fail to be directly proportional to the primary, particularly under heavy load.^[34] Transformers are therefore normally designed to have very low leakage inductance.

However, in some applications, leakage can be a desirable property, and long magnetic paths, air gaps, or magnetic bypass shunts may be deliberately introduced to a transformer's design to limit the short-circuit current it will supply.^[33] Leaky transformers may be used to supply loads that exhibit negative resistance, such as electric arcs, mercury vapor lamps, and neon signs; or for safely handling loads that become periodically short-circuited such as electric arc welders.^[35]

Air gaps are also used to keep a transformer from saturating, especially audio-frequency transformers in circuits that have a direct current flowing through the windings.^{[citation needed]}

Leakage inductance is also helpful when transformers are operated in parallel. It can be shown that if the "per-unit" inductance of two transformers is the same (a typical value is 5%), they will automatically split power "correctly" (e.g. 500 kVA unit in parallel with 1,000 kVA unit, the larger one will carry twice the current).^{[citation needed]}

[edit] Effect of frequency

Transformer universal EMF equation

If the flux in the core is purely sinusoidal, the relationship for either winding between its rms voltage E_rms of the winding , and the supply frequency f, number of turns N, core cross-sectional area a and peak magnetic flux density B is given by the universal EMF equation:^[31]

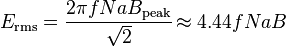
$E_\text{rms} = {\frac {2 \pi f N a B_\text{peak}} {\sqrt{2}}} \! \approx 4.44 f N a B$

If the flux does not contain even harmonics the following equation can be used for half-cycle average voltage E_avg of any waveshape:

$E_\text{avg}= 4 f N a B_\text{peak} \!$

The time-derivative term in Faraday's Law shows that the flux in the core is the integral with respect to time of the applied voltage.^[36] Hypothetically an ideal transformer would work with direct-current excitation, with the core flux increasing linearly with time.^[37] In practice, the flux would rise to the point where magnetic saturation of the core occurs, causing a huge increase in the magnetizing current and overheating the transformer. All practical transformers must therefore operate with alternating (or pulsed) current.^[37]

The EMF of a transformer at a given flux density increases with frequency.^[31] By operating at higher frequencies, transformers can be physically more compact because a given core is able to transfer more power without reaching saturation and fewer turns are needed to achieve the same impedance. However, properties such as core loss and conductor skin effect also increase with frequency. Aircraft and military equipment employ 400 Hz power supplies which reduce core and winding weight.^[38] Conversely, frequencies used for some railway electrification systems were much lower (e.g. 16.7 Hz and 25 Hz) than normal utility frequencies (50 – 60 Hz) for historical reasons concerned mainly with the limitations of early electric traction motors. As such, the transformers used to step down the high over-head line voltages (e.g. 15 kV) are much heavier for the same power rating than those designed only for the higher frequencies.

Operation of a transformer at its designed voltage but at a higher frequency than intended will lead to reduced magnetizing current; at lower frequency, the magnetizing current will increase. Operation of a transformer at other than its design frequency may require assessment of voltages, losses, and cooling to establish if safe operation is practical. For example, transformers may need to be equipped with "volts per hertz" over-excitation relays to protect the transformer from overvoltage at higher than rated frequency.

One example of state-of-the-art design is those transformers used for electric multiple unit high speed trains, particularly those required to operate across the borders of countries using different standards of electrification. The position of such transformers is restricted to being hung below the passenger compartment. They have to function at different frequencies (down to 16.7 Hz) and voltages (up to 25 kV) whilst handling the enhanced power requirements needed for operating the trains at high speed.

Knowledge of natural frequencies of transformer windings is of importance for the determination of the transient response of the windings to impulse and switching surge voltages.

[edit] Energy losses

An ideal transformer would have no energy losses, and would be 100% efficient. In practical transformers energy is dissipated in the windings, core, and surrounding structures. Larger transformers are generally more efficient, and those rated for electricity distribution usually perform better than 98%.^[39]

Experimental transformers using superconducting windings achieve efficiencies of 99.85%.^[40] The increase in efficiency can save considerable energy, and hence money, in a large heavily-loaded transformer; the trade-off is in the additional initial and running cost of the superconducting design.

Losses in transformers (excluding associated circuitry) vary with load current, and may be expressed as "no-load" or "full-load" loss. Winding resistance dominates load losses, whereas hysteresis and eddy currents losses contribute to over 99% of the no-load loss. The no-load loss can be significant, so that even an idle transformer constitutes a drain on the electrical supply and a running cost; designing transformers for lower loss requires a larger core, good-quality silicon steel, or even amorphous steel, for the core, and thicker wire, increasing initial cost, so that there is a trade-off between initial cost and running cost. (Also see energy efficient transformer).^[41]

Transformer losses are divided into losses in the windings, termed copper loss, and those in the magnetic circuit, termed iron loss. Losses in the transformer arise from:

Winding resistance

Current flowing through the windings causes resistive heating of the conductors. At higher frequencies, skin effect and proximity effect create additional winding resistance and losses.

Hysteresis losses

Each time the magnetic field is reversed, a small amount of energy is lost due to hysteresis within the core. For a given core material, the loss is proportional to the frequency, and is a function of the peak flux density to which it is subjected.^[41]

Eddy currents